Solomon is currently a student at the University of Pennsylvania where he is pursuing a Ph.D in Computer Science. He has a keen interest in all things Computer Science and Maths, so he decided to specialize in Programming Languages, an area which applies ideas from diverse areas of Computer Science, Mathematics and Philosophy. One of his favourite things is when connections are made between seemingly disparate areas of inquiry, so he has enjoyed reading the Graphical Linear Algebra blog for the connections between string diagrams and linear algebra. As the Lindström-Gessel-Vienot Lemma shows us, there is also a surprising combinatorial connection. Such occurrences make Solomon very happy!
Consider the familiar diagram for the matrix
:

Suppose that we wanted to push some flow from the input nodes and
to the output nodes
and
. Moreover, we want to do this in such a way that every output node receives some flow without any congestion in the network. More specifically, want to push flow from the input nodes to the output nodes in such a way that:
- no two different paths that are part of the flow intersect at
a vertex (not even endpoints), and - for each output node
, there is a path from some input
nodeto
.
For example, in the diagram above, we can push units of flow from
to
and
units of flow from
to
.

We can also push units of flow from
to
and
units of flow from
to
.
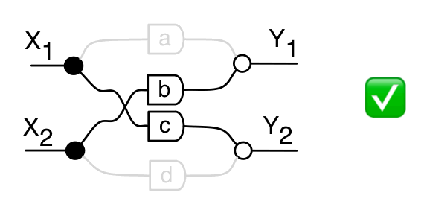
We are not allowed to push units of flow from
to
and
units of flow from
to
, since then we would have two different paths intersecting at
.

Also, we are not allowed to push only units of flow from
to
, since then there is no path from some
to
.

We call a flow that satisfies conditions (1) and (2) a viable flow. Now we will measure the signed weight a viable flow. The weight of a viable flow is simply the product of all weights on the edges that are part of the flow. To get the signed weight, we multiply the result by -1 if the flow links to
. Otherwise, we multiply the result by +1.
For example, in our matrix example, the first viable flow has weight
. The unsigned weight of this flow is
since we push
units of flow from
to
and
units of flow from
to
. To get the signed weight of this flow, we multiply the unsigned weight
by +1 since
is linked to
. A similar computation shows that the signed weight of the second viable flow is
.
Interestingly, when we add signed weights of all the viable flows in the diagram, we get the determinant of the matrix associated with the diagram i.e. . Coincidence?
The Lindström-Gessel-Vienot Lemma (LGVL) tells us that this in fact is not a
coincidence. Specifically, LGVL associates to each finite directed acyclic
graph (dag) a matrix whose determinant is exactly equal to the
sum of the signed weights of the viable flows in . To make this relationship precise we shall give the statement of LGVL, but first we need to introduce some definitions and notation that we will need in order to give the statement of the theorem.
First, we introduce permutations. For any sets and
we call any bijection
a permutation from
to
. Now assume that
sends
to
respectively. For example, let
, and let
send
to
respectively. Write
in a row in that order, skip a line, then write
below
for each
. Draw a line from
to
, and count the number
of crossings in between the
s and the
s. Define the sign of
be
. For the permutation
we have just described, there are six crossings, so the sign of the permutation is
.

The sign of a permutation can also be computed by raising -1 to the
number of inversions of
, where
is the number of ordered pairs
such that
but
. In the example above, the number of inversions of
is 6 =
, which gives the same result as before.
For the next few pieces of notation as well as the statement of LGVL, assume that is a finite directed acyclic graph. Assume further that
has input nodes
and output nodes
.
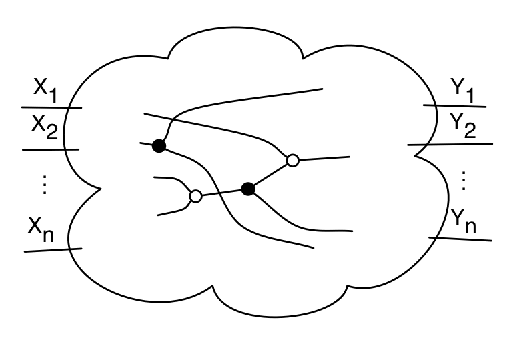
As before, we are interested in viable flows, i.e. flows that have the property that:
- no two different paths that are part of the flow intersect at
a vertex (not even endpoints), and - for each output node
, there is a path from some input
nodeto
.
Each viable flow can described by an -tuple
of paths , where
is a path from the input node
to the output node
for some permutation
. Let
be this permutation.
For each directed path between any two vertices in
, let
be the product of the weights of the edges of the path. For any two vertices
and
, write
for the sum
where ranges over all paths from
to
.
We are finally in a position to give the statement of LGVL, which is that
where ranges over all viable flows in
!
LGVL holds for any finite directed acyclic graph, not just graphs that look like the example. For example consider the following graph:

or equivalently, the following string diagram:
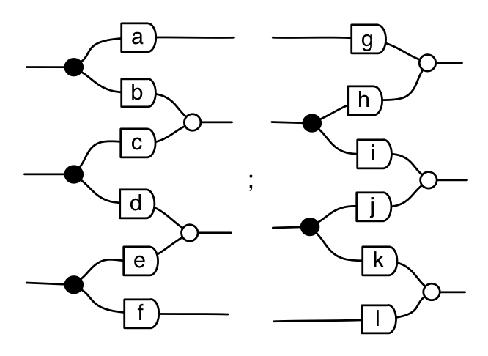
The matrix for this is
It has determinant , and it is easy to check that each of these terms indeed gives a viable flow from the
s to the
s. Note also that the sign of each term is +1 since
is sent to
in each of the viable flows.
Now on the one hand, LGVL gives us a way of computing the sum of the signed weights of viable flows in a dag as the determinant of a certain matrix. On the other hand, given a matrix , we may compute the determinant of
by doing the following. First, we find a special dag
. Next, we find a set of input vertices
and output vertices
in
. We check to see that
. Then, we (easily!) compute the sum of the signed weights of viable flows in
from
to
. Finally we conclude that the result is equal to the determinant of
by LGVL. This compositional approach to computing the determinant often leads to useful and surprising results, as we shall see below.
Consider the determinant of the following matrix:
where denotes the greatest common divisor of
and
.
It is difficult to come up with a closed formula for this determinant by using say row-reductions or the co-factor expansion. However, using the strategy involving LGVL gives a simple and surprising result.
But first, a few more definitions! Given any positive integer , let
denote the number of positive integers less than or equal to
which are relatively prime to
. For example,
since the only numbers less than 6 that are relatively prime to 6 are 1 and 5. On the other hand
since all the positive integers less than 7 are relatively prime to 1. In fact, it is easy to see that
for any prime
.
Also, for the purposes of the proof, we shall need to use the fact that
which is a property first established by Gauss. For example
Now we proceed to the actual computation. Consider the graph which has
vertices:
are the input vertices,
are the output vertices and
are intermediate vertices. If
divides
, put the edge
with weight
and the edge
with weight 1.
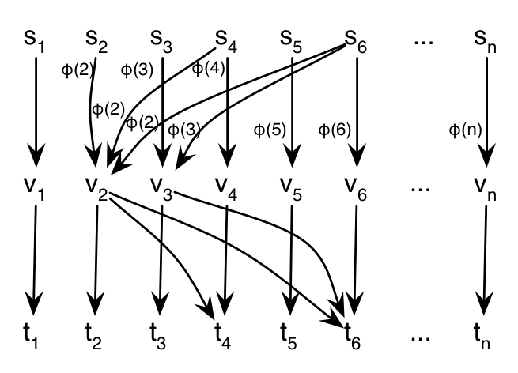
What is the weight of all the paths from
to
? Well each path from
to
can have only two edges: an edge
of weight
and an edge
of weight 1, for some
, where
divides
and
divides
. Of course the weight of this path is
multiplied by 1, which is just
. Therefore,
The last equality is justified by Gauss’ result.
By the LGVL, it follows that
where ranges over all viable flows from the input vertices
to the output vertices
.
Now the only path from to
is
since 1 has only one divisor, namely 1. As a result, for each prime
, any path from
to
in a viable flow must pass through
. This is because
has only two divisors, namely 1 and
, but the path through 1 has already been blocked by 1.
Consequently, for any product of two primes, any path from
to
must pass through
. Repeating this argument for all the other numbers less than or equal to
, we conclude that all the viable flows from
to
link
to
.
Now if there is a viable flow which links to
for some
, then there must be some
such that
is linked to
with
(why?). But this means that
divides
, a contradiction since
! So we must have
, for all
.
Thus, there is a unique viable flow from to
i.e. the flow for which
is sent to
via
. Thus, we conclude that the determinant of
is
, since the weight of each path
in this flow is
as we showed earlier:

Cute!
LikeLike
Sweet. Thank you for sharing this!
I noticed two minor typos (omitted words) and had a few questions.
“signed weight a viable flow” –> “signed weight of a viable flow”
“Each viable flow can described by” –> “Each viable flow be can described by”
I think the variable P is overloaded between this and the following paragraphs (as both an arbitrary viable flow and an arbitrary path between two given endpoints). Am I missing something, or are these actually distinct objects?
You pass lightly over a potentially interesting point: “…given a matrix M, we may compute the determinant of M by doing the following. First, we find a special dag G…” Is this inverse operation always possible?
LikeLike
Oops. I messed up. “be can” –> “can be”. 🙂
LikeLike
”It has determinant agciek + agcifl + agdjfe + bhdjfe, and it is easy to check that each of these terms indeed gives a viable flow from the {s_i}’s to the {t_i}’s.“
should be
”It has determinant agciek + agcifl + agdjfl + bhdjfl, and it is easy to check that each of these terms indeed gives a viable flow from the {s_i}’s to the {t_i}’s.“
LikeLike
Hi Pawel. Thanks for this beautiful blog!! I have learned and enjoyed a lot.
I am a newbie on this matter. I hope someday you can explain us, in your diagrammatic picture, the characteristic polynomial and trace invariants for the Hermitian case. Are your diagrams connected with the so-called trace diagrams?: https://mathoverflow.net/questions/6139/how-can-i-learn-about-doing-linear-algebra-with-trace-diagrams
Thank you in advance !!
LikeLike