Before we get started, I have a little rant. I know that some people are getting sick of these. If that includes you, dear reader, then you can safely skip it and move on to the content, below the horizontal line.
I’ve publicised this blog on Facebook and I’ve received some very interesting comments and suggestions from friends and colleagues. Several people have told me to be more concise. I also posted a link to this blog in a comment on reddit. What happened next was … surprising. The blog got over 3000 hits. In the reddit discussion I had some nice comments, some suspicions as to whether I’m a crank, and a polite suggestion to be more concise.
I understand the point about conciseness. But non-mathematicians maybe don’t. Let me explain for them: when students learn about mathematics at university level, they learn to read mathematics. Reading mathematics is not like reading ordinary prose; it takes much, much more time. You read a book chapter once, you do some exercises, you re-read certain parts again, do some more exercises, and so on, until the concepts are crystal clear. Back when I was at Sydney Uni, thinking about doing a PhD in maths, I was getting through maybe about 10 pages a day. That was a full work day.
The beauty in conciseness is that once you’ve understood the concepts and need to look up some definition or result, you don’t have to wade through paragraphs and paragraphs of lengthy monologues and explanations. The best books and papers are clear and to the point. A classic example is Atiyah MacDonald: it’s a wonderful book, brutally concise and extremely useful to have on your bookshelf as a reference.
There are two reasons for why I’ve chosen to write like this. One is that I want to try to explain my work to family, friends and colleagues who are not mathematicians. I think that, for the most part, they have no idea about what it is that I do exactly.
The other is that for the past few years I’ve been a subscriber to the London Review of Books. The London Review is amazing; its contributors are invariably incredibly talented writers who write opinion pieces, diary entries, and mainly—surprise!—book reviews. Book reviews often take the form of summarising an entire subject of study; perhaps the prose of some 18th century French author, the history of an ancient civilisation, or the contributions of some overlooked Italian painter of the quattrocento. The authors, who are usually domain experts, make their subjects extremely clear to a lay audience, but without dumbing them down. They take all the space they need and they respect their readers.
I’ve learned many interesting things from the London Review. I’ll give you an example: I’ve learned about Lucien Febvre, and his work on the question of whether Rabelais was or was not an atheist (believe me, it’s much more exciting than it sounds!). That particular book review stayed on my mind and I eventually found Febvre’s book in the library. Febvre’s ideas completely changed the way I understand the concept of history. I don’t think I would have ever found Febvre if not for the London Review: most of my friends have PhDs in Computer Science!
I wish the London Review featured more articles about maths and science, because I’m not really a big fan of “popular mathematics”. All too often it is written by specialists of “popular science writing”. They like to focus on the personalities, their sex lives, and their habits of writing on windows with coloured markers à la “A Beautiful Mind”. When they finally get around to the maths we often get a bunch of vague analogies, an equation or two, maybe with some fuzzy claims tagged on to the end. This blog is a challenge to see if I can manage to explain some of the maths I’ve been working on for the last few years to a lay audience, but without dumbing it down. For that to work, conciseness must be sacrificed, just like it is sacrificed in the wonderful articles of the London Review. I just wish I had half the talent of those writers!
I’m going to assume that you’ve heard of Lego. Suppose that we have a large collection of the following kinds of bricks to play with.
In Lego terminology (yes, there is such a thing) they are actually not called “bricks”. The things with the Lego-branded bumps on the top are called plates. This is because the word “brick”, in Lego nomenclature, is reserved for their taller cousins, which are the height of three plates, stacked on top of each other. The bumps on top are called studs, by the way. The purple thing without the studs is called a tile — it has two holes for studs underneath but no studs on the top. But we are going to talk about something much more interesting than—let’s admit it—somewhat nerdy names for toys. So, at the risk of upsetting Lego purists, we will just call them bricks from now on.
I’m going to describe an algebra, a little mathematical language that we will use to describe Lego constructions. First, let’s turn all the bricks and put them on their sides so that they look like this.
The algebra consists of two operations. You’ve already seen an example of an operation, addition, in the previous episode. Addition takes two arguments, and has one result. The two Lego operations also take two arguments and have one result. Differently from addition, the arguments are not numbers but Lego constructions. The result of performing each operation will also be a Lego construction.
The first operation’s name is ‘⊕’, and we will call it the direct sum in English. Direct sum works simply by putting the Lego construction in the first argument above the lego construction in the second argument. Let’s look at a few examples, using the simple kinds of bricks in our collection.
Notice that, differently from ordinary addition, the direct sum is not commutative! The two examples above are a case in point; swapping the arguments results in different constructions. You may object that the results are actually the same: if I flip the first, I get the second. The number of holes and studs is the same. Nice thinking, and I like the cut of your jib.
This is a very important point, so let’s spend a minute on it. Using direct sum, we can construct a column of bricks, stacked on top of each other. So suppose for a second that we considered the two results above to be equal. They are, respectively, the first arguments in the following two examples.
So if we made that judgement call, then we would also have to consider these results to be equal. Here’s a proof, where we put the question mark on the initial, questionable assumption.
Long story short, considering direct sum to be commutative results in completely forgetting the order of the bricks in any stack of bricks constructed using it. But the order that they are stacked in is crucial, we cannot forget it. We need to know it because of the second operation, which allows us to connect bricks together by fitting studs into holes. If we forgot the order, we wouldn’t know which holes to fit which studs in!
The second operation, named ‘;’, is called composition in English. It is a little bit more complicated than direct sum: it only works on constructions that can be connected perfectly. A perfect connection means that the number of studs sticking out of the first argument is exactly the number of stud holes in in the second argument. For example:
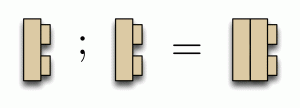
Like the direct sum, composition is not commutative, as the following examples demonstrate. Thus, unlike addition, the order of the arguments matters.
Here’s another example.
The reason why the composition operation ( ; ) is a little bit more tricky than direct sum ( ⊕ ) is demostrated by the example below, in which the composition is not defined.
Clearly, in real Lego, I could make a construction by attaching the short purple brick to the long red brick. I would have to tell you, however, which of the red brick’s studs to use, and there are four different possibilities. Composition does not want to bother with possibilities, it simply gives up: in the example above, composition has no result on those particular arguments. Our Rules of the Game declare that the expression simply does not make sense, similarly to how it doesn’t make sense to add 2 kilograms to 2 meters.
How could we make this a little bit more precise? It’s pretty simple. We can associate a pair of natural numbers (non-negative integers) to each Lego construction. The first number tells us how many stud holes it has, the second how many studs. We do this for the basic bricks below.
Next we have rules that associate this information to more complicated constructions. First, for the direct sum:
Let me explain what this rule says. First the structure of the rule: you should read everything above the horizontal line as the assumptions, and the thing below the line as the conclusion. So the rule says that, assuming X is a Lego construction with k holes on the left and l studs on the right, and that Y is a Lego construction with m holes and n studs, then X ⊕ Y will be a Lego construction with k + m holes and l + n studs. Since we know that ⊕ works by putting the first thing on top of the second thing, this is pretty obvious, right?
Next, the rule for composition looks as follows.
It says that composition X ; Y is defined provided that the number of studs of X is equal to the number of holes of Y. As well as rejecting our previous attempt to connect the purple 1×1 brick to the red 1×4 brick, the rule also forbids us from performing the following composition.
This is maybe a bit unexpected because in real Lego we can, of course, make a construction by connecting bricks of these shapes. But as we said, we only want to allow the connection if it is perfect, and here the second argument has more stud holes than the first argument has studs.
We now have a language for describing some Lego constructions in terms of their basic bricks. For example
and
Some of you are probably squinting a little bit at the screen. Something is not quite right with this story. I’ll come clean, I haven’t really been talking about Lego at all, but about magic Lego. Right after these (optional) messages.
When I was a kid in Poland, in the mid 1980s, I totally loved Lego. I still do, although probably I don’t quite qualify as an AFOL. But back then, I was obsessed with the stuff. Some background: Poland in the 1980s was still officially communist, although nobody actually ever believed a word of it, not the people in power, nor the people on the street. Everybody was, more or less, waiting for the system to crumble. It was only a matter of time. The economy was a joke, the black market was booming, and somehow the people got by.
I’ve spent the last 25 years of my life trying to convince people that my childhood wasn’t as grey and miserable as they imagine. It was pretty awesome, actually. My parents earned something like $50 a month, in “hard currency”. Of course, in the local currency the buying power was much more. It was enough for all the basic necessities, although toilet paper was always a challenge, for some reason. Something like Lego, though, had to be paid for in hard currency. Nevertheless, I got Lego for Christmas most years — and I have no idea how my parents managed it.
Once, I think I was 8, I sent a fan letter to the Lego factory in Denmark. My dad helped me with the English. A few weeks later I got a lovely reply, together with a few sheets of Lego stickers that I put all over my exercise books. My schoolmates were dying of jealousy, and my love for Lego was made everlasting. By the way, this was 1980s Lego. Back when it was ok for girls to play too. Before they branched out into “Lego Friends” and other such atrocities. My little sister played with (ordinary) Lego, and GI Joes, but she played with Barbies too. She’s now a gender-informed historian at Monash Uni in Melbourne. Go figure. Talking about my sister, I should plug her latest book. It’s very interesting. Just kidding, it’s great!
Here’s where there are some problems with what we’ve been saying so far. The rule for composition tells us that we should be able to make sense of composing any two constructions where the number of studs in the first argument is equal to the number of holes in the second. But this is a problem for ordinary Lego, because how do we make sense of the following?
Our rule says that this composition should be allowed, because the number of the studs of the first construction is equal to the number of holes of the second. This is where the magic comes in. In magic Lego, the result is as follows.

During composition, the second brick magically grew so that its two stud holes were in the right place to fit into the studs of the first argument. But the magic does not stop there; the following is also true, in magic Lego.
Here the second argument stays looking the same, but the edge of the first contracts so that the two studs fit into the holes of the second argument. But how can both of these be true? Well, in magic Lego the two results are considered to be the same thing.
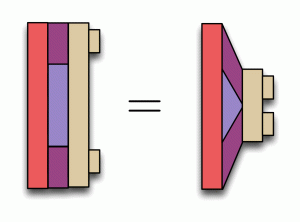 This may seem a bit mysterious, but it you think about it, the building instructions are the same in both cases: the same studs are going in the same holes. You can get from one to the other by deforming the bricks, as if they were made of rubber. In summary: what matters in magic Lego is not the size or shape of the bricks — just how they connect to other bricks.
This may seem a bit mysterious, but it you think about it, the building instructions are the same in both cases: the same studs are going in the same holes. You can get from one to the other by deforming the bricks, as if they were made of rubber. In summary: what matters in magic Lego is not the size or shape of the bricks — just how they connect to other bricks.
Similarly, the following happens.
Here the second argument grows so that the holes and the studs line up in the result. As you can see, in magic Lego, we can’t tell the difference between plates and bricks. We will see how all of this is related with diagrams in the next episode.
Continue reading with Episode 5: Spoilers, Adding (Part 2) and Zero.



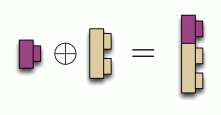










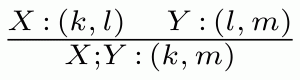

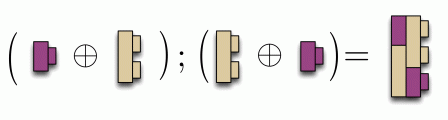
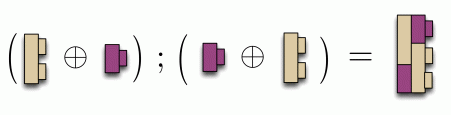


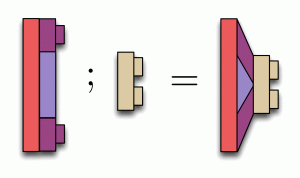

Just a quick note to let you know that I am enjoying your blog and hope that you will keep writing it!
LikeLiked by 1 person
+1
LikeLike
I tried leaving a comment and your provider said “enter a valid email” although I’m sure I did. I just wanted to let you know I was seeing that issue.
LikeLike
I posted a comment on HN that I was excited for your blog (engineering background) but wanted to get to the “meat” and I feel like this episode got there. Keep up the good work; I’ll be anxiously awaiting more.
LikeLike
Thanks Josh — there’s plenty more meat to come, this is just a taster 🙂
LikeLike
Love your writing, kudos!
LikeLiked by 1 person
Excellent! Looking forward to more posts!
LikeLiked by 1 person
Fantastic post, Pawel!
LikeLiked by 1 person
Thank you for taking the time to to expand on the mathematical thought process behind your conception and intuition of linear algebra. Please keep up the good work
LikeLiked by 1 person
I agree completely!
This is awesome, well written and I love how you “unpack” those rules/operations into plain English.
Eye-opening and dot connecting 🙂
LikeLike
Actually, your lack of conciseness is delightful 🙂
LikeLiked by 2 people
Thanks!
LikeLike
I don’t remember last time I’ve read an entire article, let alone a series. Your writing is captivating, and please continue it.
But give us some short term goal about what an audience(lay or anyone – I am a CS student) should get out of the series(i.e. you will understand xyz at the end of 10th article) – It will be relaxing.
I am itching to know how would fit with my existing knowledge.
LikeLiked by 1 person
That’s a nice idea, thanks! — I’ll think about including a rough plan in the next episode.
LikeLiked by 1 person
http://www.lrb.co.uk/v02/n06/peter-burke/rabelaiss-box
Is that the link to the article? I enjoyed reading it indeed.
LikeLike
Hi Alexander,
Thant’s not it, but I agree that it’s nice. It’s weird, but I can’t find a link to the article on the lrb archive, but I’m pretty sure it’s this
http://www.nybooks.com/articles/archives/1983/mar/31/which-side-was-rabelais-on/
Maybe it was reprinted in a print version of the magazine but does not appear in the archives?
LikeLike
The rule for direct sum looks commutative, both in holes and in studs. I don’t follow how the visual logic maps to the rule. Please help
LikeLiked by 1 person
Thanks a lot for this comment! I had a feeling that I was explaining that bit a bit too quickly.
I’ll let you know when I’ve fixed it.
LikeLike
I expanded the explanation now, I hope that it helps!
LikeLike
Hello. I hope it is not too late to comment on this. I have 2 things I am stuck on, trying to understand the non-commutativity of the direct sum:
1. I do not get why we have to make a note of the ordering of the direct sum in order to allow for the composition.
It looks like with the magic lego, constructions can be composed provided the number of studs and holes is the same, irrespective of the position of the front layer of studs corresponding to the order of the elements of the direct sum.
2. With the rule in symbolic notation for the direct sum, X+Y: (k+m,l+n), the “k+m” and “l+n” bit look like regular addition, which seems commutative. I don’t see how the non-commutativity comes out of that.
Any clarification would be very greatly appreciated!
I love your blog – Thank you so much for making it!
LikeLike
Thanks for the questions!
First your point 2: you are right, it is true that X+Y and Y+X have the same numbers of studs and holes. But they are, in general, different, which brings us to your point 1.
Let’s suppose that we want to consider X+Y and Y+X to be equal. if X and Y are simple bricks then this seems reasonable, since we could say that one is the other “rotated”. But this idea breaks down when we direct sum with a third brick, like in the second example where we direct sum with the purple tile. We start with two things that we would consider equal, and direct sum them with the third tile, obtaining two constructions which are no longer related by this idea that one is the other rotated. We could still go on trying to think that the two three-brick constructions are the same, but the upshot would be that when we do a composition we’d have no idea about which stud is fitting into which hole.
So the deeper reason why direct sum must not be commutative is that we need to know about precisely which studs fit into which holes when we do a composition. And this is why in all of our diagrams the order of the dangling wires matters, and why we have explicit diagrams that permute them for us. In the world of matrices, this means that the order of the rows and the columns of a matrix matters: I can’t just jumble up a matrix by arbitrary swapping rows and columns: I get a different matrix.
Non-commutativity is one of these things that we find weird because most of our early experience of maths is with commutative operations. I will write an episode about this very soon.
Let me know if this helps: also, let me know if you think of a way I could explain it better in the article!
Thanks for reading 🙂
LikeLiked by 1 person
Thank you so much!!! I think I understand now: So in the case of the magic lego, with the 2 alternatively stretched diagrams being equal – it would not be generally acceptable for the lego to stretch in such a way so the stud fitted into the bottom hole and the bottom stud went into the top hole.
Or, in the case of wires, non-commutativity would mean it doesn’t matter which output wires go to which inputs. So in the recipe analogy you give later on, if you switched the position of the sugar and the mascarpone, non-commutativity would say that would be fine, but the result of our final crema di mascarpone would not taste fine, or at least, it would necessarily taste the same.
I think I got confused because I couldn’t see how the two three-brick constructions were different if we had already assumed that the original two differently ordered constructions were the same, and also with the magic lego constructions that looked different but were the same, I didn’t realise that the important thing was the order of studs to holes was still maintained in both cases.
In hindsight, I actually think you explained it really well in the article. I am just extremely easily confused!
Thank you so much for taking the time to reply and for such a detailed, patient and clear response! 😀
LikeLiked by 1 person
That’s right: it’s the order of the studs/wires that is the important bit!
And don’t worry about being confused, I’ve been giving talks to academic audiences about related things for several years and the non-commutativity is something *extremely* difficult for people to stomach. I practically always get questions about it. It almost seems that some people actually get annoyed about using non-commutative operations!
By the way, one way to keep commutativity is to give all the studs/wires individual names, but in my opinion this really makes things a lot harder (and uglier): you have to keep inventing new names, renaming, “hiding” names when you compose etc etc. But this is the more traditional approach, at least in computer science, and is much, much more common. I’ll get around to discussing this issue one of these days.
Anyway, thanks for the great feedback 🙂
LikeLiked by 1 person
This is really great stuff. Cheers!
LikeLike
just a correction: “As well as rejecting our previous attempt to connect the purple 1×1 brick to the red 1×4 brick” should be “… the red 4×4 brick…”, right?
LikeLike
You have a point; I was thinking of it as a 1×4 brick because it has “width 1” and “height 4”. But thinking of Lego as a precursor to the algebra of matrices, it probably would have made more sense to say that it’s 4×4, where mxn means “n holes” and “m studs”.
LikeLike
I was also thinking about that, but then I was confused in the magic lego part, trying to picture them as matrices was no longer possible for me, because instead of being non existant it has multiple solutions.
LikeLike
This reads like a mystery story written by Jorge Luis Borges! I’m engrossed.
LikeLiked by 1 person
Pavel, would you mind sharing what tool did you use to create lego graphics?
LikeLike
Thank you for this wonderful blog series, I’m pretty excited about what comes next 🙂
But here comes a question: what mathematical abstraction describes the ordinary Lego, not the magic one?
The one where it is ok to have 4 possibilities when connecting 1-plate to 4-plate.
The same question is applicable to any other construction set, like Zoob – where there is always a number of ways to connect parts, and it grows combinatorially with the size of assembled parts (or better the number of free connectors of different types)?
LikeLike
Hey Pawel,
Great post! I used Legos to teach categories, operads, and algebras to folks, including people at SIemens, and was surprised all kinds of subtleties you run into and can have fun figuring out various ways around (i.e. magic legos). I think there is a lot of pedagogical potential here still untapped.
I second the comment above asking how you made the Lego graphics.
LikeLike