Chapter 12 of Fibonacci’s Liber Abaci is full of compelling problems. One is called “On two men with fish and the customs agent”. Another is a riddle about a man who visits a pleasure garden – accessible through seven guarded doors – where it’s possible to collect apples. You can enter freely, but on your way out you must pay each of the seven guards a tax: half of the apples you’re carrying, plus one additional apple.

Artistic impression of Fibonacci’s pleasure garden. The tax at this door is 10/2 + 1 = 6 apples.
So, Fibonacci asks, how may apples does the man need to collect in the pleasure garden so that he gets to take one apple home? (spoiler: 382).
Given Fibonacci’s trading roots, his obsession with tax and customs duties is understandable. Without doubt, however, the most famous part of the chapter is not about taxes. It’s a very short exposition entitled “How many pairs of rabbits are created by one pair in one year”, and it starts as follows:
A certain man had one pair of rabbits together in a certain enclosed place, and one wishes to know how many are created from the pair in one year when it is the nature of them in a single month to bear another pair, and in the second month those born to bear also.
Fibonacci doesn’t tell us the name of the certain man. It will become boring to refer to him repeatedly as “the certain man”, so from now on we will change his gender to female and refer to her as Giusy (pronounced Juicy), short for Giuseppa the Rabbit Breeder.
The following helpful table is included in the margin, with the number of rabbit pairs for each month
 |
beginning |
1 |
| first |
2 |
| second |
3 |
| third |
5 |
| fourth |
8 |
| fifth |
13 |
| sixth |
21 |
| seventh |
34 |
| eighth |
55 |
| ninth |
89 |
| tenth |
144 |
| eleventh |
233 |
| twelfth |
377 |
and the procedure for calculating the successive entries is explained as follows
You can indeed see in the margin how we operated, namely that we added the first number to the second, namely the 1 to the 2, and the second to the third, and the third to the fourth, and the fourth to the fifth, and thus one after another until we added the tenth to the eleventh, namely the 144 to the 233, and we had the above written sum of rabbits, namely 377, and thus you can in order find it for an unending number of months.
This sequence of numbers in the table
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … ①
is now known as the Fibonacci numbers. As Fibonacci explains, starting with F0 = 1 and F1 = 2, we obtain successive entries by recursively calculating
Fn+2 = Fn+1 + Fn.
This famous series—and the related golden ratio–are the absolute bread and butter of popular mathematics. Many facts, factoids and myths involving pineapples, pine cones, aesthetically pleasing rectangles, renaissance paintings etc. have been assigned to them. They spice up the otherwise vapid pages of Dan Brown novels. As well as books, there are hundreds of videos on YouTube. While many are terrible, there are some gems: for example, this lecture by Keith Devlin is very good since he manages to be engaging, while at the same time challenging some of the most egregious numerological pseudo-science.
In modern presentations, Fibonacci’s famous sequence is usually given as
0, 1, 1, 2, 3, 5, 8, 13, 21, … ②
or
1, 1, 2, 3, 5, 8, 13, 21, 34, … ③
We will stick with Fibonacci’s original version ①. There’s a good reason for this: Giusy’s first couple of rabbits start breeding already in the first month. So if the first rabbit couple was delivered one month late, Giusy would observe the following series
0, 1, 2, 3, 5, 8, 13, 21, … ④
Fibonacci’s ① starts with the third number of ② and the second of ③. But it wouldn’t really work to simply shift ② or ③ to the left: differently from ④, both ② and ③ contain the sequence 1, 1, which Giusy would never observe.
We can obtain ① by adding ② and ③. Addition works pointwise, scanning vertically, 0+1=1, 1+1=2, 1+2=3 etc, as illustrated below. As we will see, this is the way of defining addition on number sequences. We will also define multiplication on sequences, but it won’t work anything like this.

The story of graphical linear algebra so far has taken us from zero to the natural numbers, to integers and then fractions. For the next few episodes we will shift our focus of from numbers to sequences. My aim for the rest of this episode is to whet your appetite by giving you a taste of the maths that we will use. For now, it will be a high-level overview, we will not go over everything in detail.
Eventually we will discuss some applications in control theory and I will do my best to explain when we come to that, although I’m not an expert. In this episode, though, I’ll talk about computer science motivations; some of the things that I found the most interesting while playing around in this particular neck of the graphical linear algebra woods.
We start by generalising Fibonacci’s rabbit problem.
Giusy originally got a pair of rabbits. No external rabbits get added, nor any taken away at any point afterwards. So we can think of this as the following rabbit input sequence
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, …
with resulting rabbit output sequence
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
Similarly, as we have already discussed, adding the first pair one month late would mean that the shifted rabbit input sequence
0, 1, 0, 0, 0, 0, 0, 0, 0, 0, …
results in the shifted output sequence
0, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
But there’s no reason to add just one pair. For example, what if Giusy started with two pairs of rabbits? And, moreover, let’s suppose that she goes to the rabbit market every second month to buy another pair of rabbits. This rabbit input sequence would then be
2, 0, 1, 0, 1, 0, 1, 0, 1, 0, … ⑤
Following the Fibonacci principle of rabbit reproduction, we would get output sequence
2, 4, 7, 12, 20, 33, 54, 88, 143, 232, … ⑥
The reasoning is as follows: the input sequence 2, 0, 0, 0, 0, … produces the result 2, 4, 6, 10, 16, … obtained by doubling each entry of ①. Twice the rabbits, twice the breeding. Next, 0, 0, 1, 0, 0, 0, 0, … produces 0, 0, 1, 2, 3, 5, …; that is, a shifted ①. Similarly for 0, 0, 0, 0, 1, 0, 0, 0, 0, … and so forth. Adding up all of these input sequences results in ⑤, so adding up all of the result sequences results in ⑥.
We can use the same kind of reasoning to figure out what would happen if Giusy started an ambitious commercial rabbit breeding farm. Say her business plan started with investing in three pairs, then selling one pair in the first month, two in the second, three in the third, and so forth. In this case, the rabbit input sequence would be
3, -1, -2, -3, -4, -5, -6, -7, -8, -9, …
and the result is, unfortunately
3, 5, 5, 5, 3, -1, -9, -23, -47, -87, …
so it looks like Giusy’s rabbit business would collapse sometime in the fifth month: negative rabbits doesn’t sound good. To be a successful rabbit entrepreneur, Giusy needs to understand the principles of sustainable rabbit farming, which we will discover at the end of this episode.
What’s going on here, mathematically speaking?
It looks like we are defining a function that takes number sequences to number sequences. By introducing and taking away rabbits we are causing the total numbers to change. We could try to write down a formula to calculate subsequent entries in the output sequence based on previously outputted values and the current input value. But formulas are boring.
Moreover, I hope that I’ve managed to make you at least a little bit uncomfortable about the pseudo-scientific language of causality. In graphical linear algebra, relations take centre stage. Of course, it is useful to know when a relation describes a function – as we will see below – but functions are not part of our basic setup. Instead, we think of the Fibonacci rules of rabbit breeding as defining a relation between number sequences. For example, it relates
1, 0, 0, 0, 0, 0, 0, 0, 0, 0, … with 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
2, 0, 1, 0, 1, 0, 1, 0, 1, 0, … with 2, 4, 7, 12, 20, 33, 54, 88, 143, 232, …
3, -1, -2, -3, -4, -5, -6, -7, -8, -9, … with 3, 5, 5, 5, 3, -1, -9, -23, -47, -87, …
and so forth.
This relation is a kind of “ratio” between sequences. We have already seen how fractions in graphical linear algebra work and that they can be thought of as ratios. A little reminder example: the fraction 3/4 is drawn

and, seen as a linear relation, contains (4, 3), (8, 6), (-2/3, –1/2) and so on; all those ordered pairs that satisfy the ratio “three times the first number is four times the second”.
Next, a sneak preview of how we will use graphical linear algebra to capture the Fibonacci sequence ratio with diagrams.
The Fibonacci number sequence can be expressed nicely by something called a generating function. We will discover some of the underlying mathematics in the future. If you can’t wait, the classic generatingfunctionology by Herbert S. Wilf is free to download. Wilf’s Chapter 1 starts with the following, well-known simile:
A generating function is a clothesline on which we hang up a sequence of numbers for display.
The kinds of generating functions that we will use will be fractions of polynomials. So, as we will see, the generating function for ① is

the one for ② is

and the one for ③ is

If you haven’t seen this kind of thing before then this will all look very mysterious. Don’t worry, with graphical linear algebra everything will become crystal clear. At this point, just trust me: there’s a tight relationship between these fractions and the sequences that we saw previously.
I can’t resist making one remark though: look at the three fractions above. Since all of the denominators are the same, following the usual rules of addition of fractions, the first is just the addition of the second and the third, just like ① is ②+③ as sequences. Indeed, an extremely interesting and useful property of generating functions is that their algebra as polynomial fractions is compatible with the algebra of the sequences they represent.
Generating functions go back to the 18th century and Euler. I’ve always thought of them as a kind of “prehistoric” computer science, 2oo years before Turing. Indeed, computer scientists are often faced with coming up with finite specifications (e.g. programming languages, automata, regular expressions, Turing machines, …) for infinite behaviour. Generating functions are a beautiful example of this phenomenon: they are a compact, finite syntax for infinite sequences.
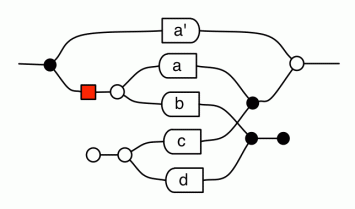
It’s time to start drawing diagrams. The following is the diagram for (1+x)/(1-x-x2), the generating function for Fibonacci’s ①.

You should recognise most of the components of this diagram, apart from all the white x‘s on black backgrounds. They are new generators, and they stand for the indeterminate x of a polynomial. Adding them and their associated equations to our graphical language will give us the ability to write down any polynomial fraction whatsoever. We will go through this properly in the next episode.
Now for a preview of the cool stuff. We already noticed that the Fibonacci sequence ratio can be seen as a function from input rabbit sequences to output rabbit sequences. It turns out that this can be observed just by looking at the diagram. In fact, we can use diagrammatic reasoning to rewire the above into the following

which can be understood as a signal flow graph, a concept to which we will devote quite a bit of time in the future. Here the left boundary can be thought of as input and the right as an output. The denominator of the polynomial has been transformed into a fancy feedback loop.
We can now this latest diagram and turn it into some code. There’s no intelligence involved, a simple procedure takes a signal flow diagram and produces code. Here’s the result in OCaml. We will go through the procedure in due course.
(* "forward" Fibonacci *)
let ffib x =
let rec ffibaux r1 r2 r3 x =
match x with
| [] -> []
| xh :: xt ->
xh + r1 + r2 + r3 ::
ffibaux xh r3 (xh + r1 + r2 + r3) xt
in ffibaux 0 0 0 x;;
If you don’t know OCaml, don’t worry, you can still cook along: open this in a fresh browser window. It’s an interactive OCaml shell running right in your browser. Copy and paste the above code into the prompt.
If everything worked as expected, you ought to get the following
val ffib : int list -> int list = <fun>
which says that ffib is a function that takes a list of integers and returns a list of integers. OCaml is nice like that, it figures out the type for you. Now paste the following
# ffib [1; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0];;
- : int list = [1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377]
which is the list of the first thirteen Fibonacci numbers, as in Liber Abaci. Say Giusy throws in one additional rabbit pair each month, then the numbers will be
# ffib [1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1];;
- : int list = [1; 3; 6; 11; 19; 32; 53; 87; 142; 231; 375; 608; 985]
You get the idea; feel free to try other inputs.
Finally, we return to Giusy’s dream of becoming a successful, sustainable rabbit breeder. She’s in luck because the original diagram can be rewired in another way, again looking like a signal flow graph but this time where the input is on the right and the output in on the left. Now it’s the numerator that turns into a feedback loop.

But it’s still morally the same diagram, the same ratio, relating the same sequences. Just that now we understand it as having its input on the right and its output on the left. Nothing wrong with that: graphical linear algebra is good with symmetries. It’s also why dividing by zero wasn’t a problem.
We can also turn the new diagram into code.
(* "backward" Fibonacci *)
let rfib x =
let rec rfibaux r1 r2 r3 x =
match x with
| [] -> []
| xh :: xt ->
xh - r1 + r2 + r3 ::
rfibaux (xh - r1 + r2 + r3) r3 (-xh) xt
in rfibaux 0 0 0 x;;
and, as a function, this now computes the inverse to ffib. So, for example:
# rfib [1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377];;
- : int list = [1; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0]
Now, let’s say that Giusy has space for 5 rabbit pairs and wants to sell off any overflow. What should her business plan look like?
# rfib [5; 5; 5; 5; 5; 5; 5; 5; 5; 5; 5;];;
- : int list = [5; -5; 0; -5; 0; -5; 0; -5; 0; -5; 0]
And we see that she ought to start with 5 pairs, sell off 5 in the first month, and every second month after that. Giusy’s happy, with both bankruptcy and rabbit plagues avoided. Graphical linear algebra saves the day again.





































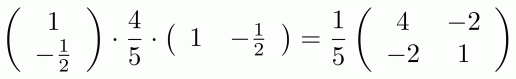













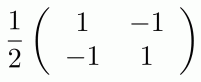






















 Our diagrams are not fragile. They are precise mathematical objects and come with a set of equations which allows us to write proofs, transforming one diagram into another. As we have seen, all of these equations have rather simple justifications and describe how an abstract operation of addition interacts with an abstract operation of copying. Hence the slogan, which we saw back in
Our diagrams are not fragile. They are precise mathematical objects and come with a set of equations which allows us to write proofs, transforming one diagram into another. As we have seen, all of these equations have rather simple justifications and describe how an abstract operation of addition interacts with an abstract operation of copying. Hence the slogan, which we saw back in 




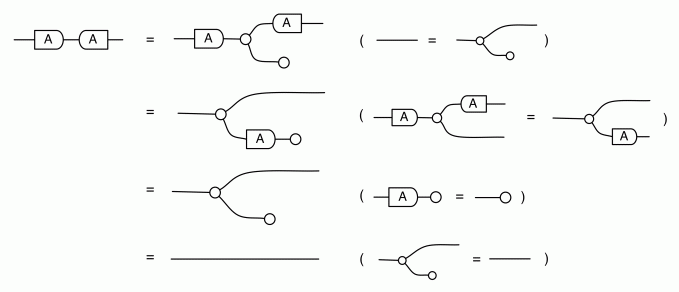




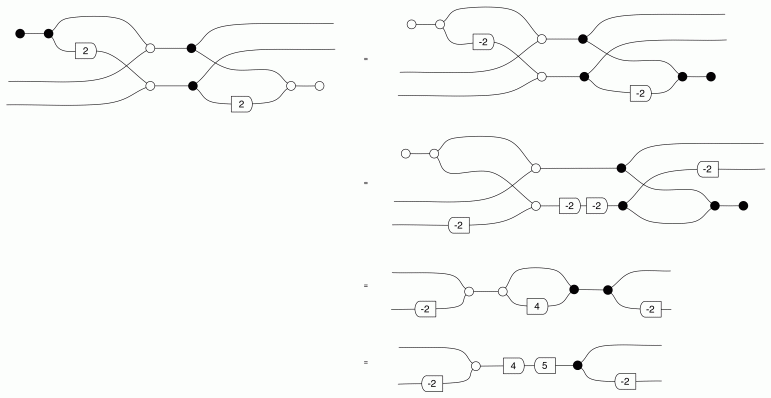
 The second equality follows from the
The second equality follows from the