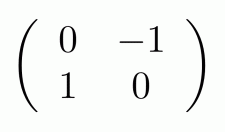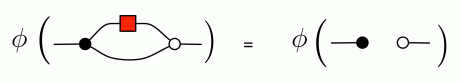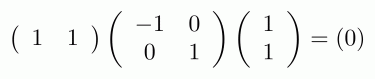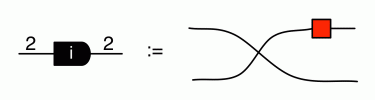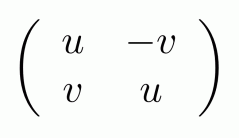In the last episode we introduced the fifth and final principal actor of graphical linear algebra, the antipode. This episode’s main task is showing that diagrams built up of the five generators constitute a diagrammatic language for integer matrices and their algebra. We will also discuss a cute example involving the complex numbers.

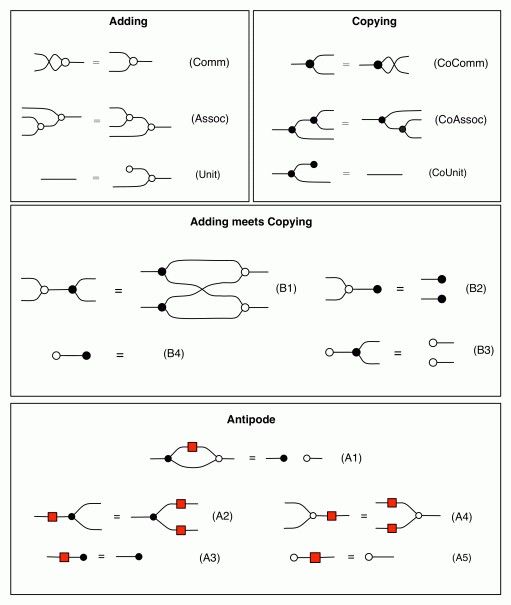
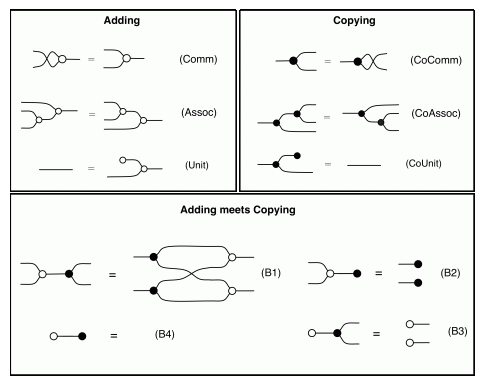
The cheat sheet for the diagrammatic system H  that includes the antipode is repeated below for easy reference.

We have already showed that H allows us to extend the syntactic sugar for natural numbers to a sugar for all the integers. We have also verified that the integer sugar obeys the usual algebraic laws of integer arithmetic. In particular, we proved that

using the equations of H and diagrammatic reasoning: this is just -1 ⋅ -1 = 1, expressed with diagrams.

 

---

 

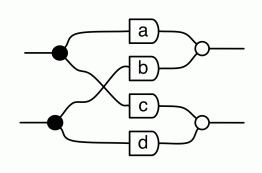
Let’s start with an example. The diagram below has two dangling wires on both sides.
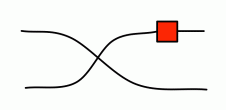As such, it ought to denote some 2×2 matrix, and to get the entry in the ith row and jth column we need to look at the paths from the jth dangling point on the left to the ith dangling point on the right.

Before the antipode entered the frame, it sufficed to count the number of paths; the current situation is a little bit more complicated because there are positive paths—those on which the antipode appears an even number of times—and negative paths, those with an odd number. To get the relevant integer entry, we need to take away the negative paths from the positive paths. So, in the very simple example above, we have exactly one positive path from the first point on the left to the second point on the right, and one negative path from the second point on the left to the first on the right. The corresponding matrix is therefore:

Actually, I didn’t choose this matrix at random: it allows us to consider the complex integers (sometimes called the Gaussian integers) and their algebra in a graphical way. We will come back to this after tackling the main topic for today.

---

 

We want to prove that H is isomorphic to the PROP Mat_Z of matrices with integer entries. The letter Z is often used to mean the integers, from the German word Zahl meaning number; this notation was apparently first used by Bourbaki.

Mat_Z is similar to the PROP Mat that we discussed in Episodes 12 and 13: the arrows from m to n are n×m matrices, and just like before composition is matrix multiplication. The monoidal product is again direct sum of matrices.

The proof H ≅ Mat_Z (the symbol ≅ is notation for isomorphic to) is similar, and not much more difficult than the proof, outlined in Episodes 15 and 16, of B ≅ Mat. Let’s go through the details.

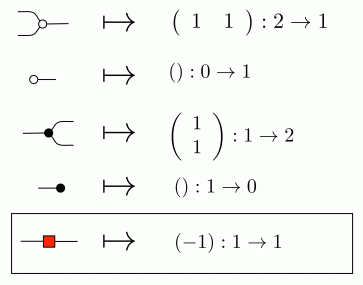
First we define a homomorphism of PROPs from H to Mat_Z. Let’s call it φ, the Greek letter phi. Since both H and Mat_Z are PROPs, and H is a free PROP built from generators and equations, it is enough to say where φ sends all the generators, and then check that the equations of H hold in Mat_Z.

It turns out that φ works the same way as θ for all of the old generators. The new part is saying where the antipode goes, and not surprisingly, it is taken to the 1×1 matrix (-1). Like so:

For φ to be well-defined, we need to check that all the equations of  H also hold in Mat_Z. Fortunately, most of that work was already done for θ, we only really need to check the new equations that involve the antipode. Let’s check the most interesting of these, (A1); we need to calculate whether the following is true:

This amounts to checking if

and it does, indeed, work. The other equations, (A2) through to (A5) are similarly easy computations and we will skip them; but feel free to check!

---

 

So we have a homomorphism φ: H → Mat_Z. To show that it is an isomorphism, we will show that it is full and faithful. Fullness—the fact that every matrix has a diagram that maps to it via φ—is the the easy part.

First, we need to check that the sugar that we defined in the last episode works with φ as expected, which is confirmed by the following simple calculation:

Any matrix with integers as entries can now be constructed following the procedure described in Episode 15. We will skip the details, as it is all pretty straightforward! The upshot of the construction is that we can extend the sugar for natural number matrices to a sugar for integer matrices: given an m×n integer matrix U we obtain a sugar

such that

This establishes that φ is full.

---

 

So what about faithfulness, the property that says that whenever two diagrams map to the same matrix then they must already be equal as diagrams?

The trick is to get our diagrams into the form where the

copying comes first, then the antipodes, then the adding  (★)

One way of doing this is to use the theory of distributive laws. Eventually we will go through all of this properly, but for now I will just give you a high-level executive overview. The main insight is that we have three different distributive laws, the first involving the adding and the copying (B1)-(B4), the second the antipode and copying (A2)-(A3), and the third the antipode and adding (A4)-(A5).

The three distributive laws, are compatible with each other in a sense identified by Eugenia Cheng in her paper Iterated distributive laws. The fact that the distributive laws play together well in this way gives us the factorisation (★) that we want. We will discuss Cheng’s results in more detail in a later episode. Incidentally, she has recently written a book about category theory and recipes; I wonder if she knows about Crema di Mascarpone!

---

We could also try a rewriting argument, taking for granted that the rewriting system described in Episode 16 terminates.  Adding the following rules

it seems that the expanded system ought to terminate also, although I have not yet got around to proving it. These termination proofs are always really messy for a rewriting amateur like me; I would love to hear from an expert about how to do these kinds of proofs in a nice way.

---

 

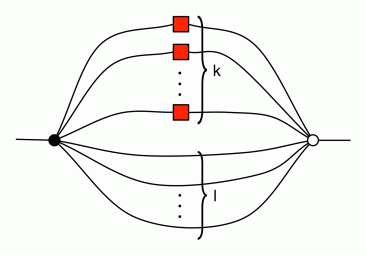
Once we know that every diagram can be put in the form (★), the proof of faithfulness is fairly straightforward. We start with those diagrams that have one dangling wire on each side. Every such diagram in the form  (★)  is either the sugar for 0 (a single discard followed by a single zero) or it can be rearranged into the form:

for some natural number k of wires with one antipode and some natural number l of wires with no antipode. This is because we can always get rid of redundant discards and zeros with (Counit) and (Unit), cancel out multiple antipodes in series using (†), then rearrange, and eat up any annoying permutations with the iterated copy and add sugars.

Once our diagram is in this form we can desugar and repeatedly use (A1), each time destroying one pair of antipode wire and no-antipode wire. Either we end up with no antipodes left, in which case the diagram is equal to a non-negative sugar, or we end up with some number of antipode wires. In the latter case, we can use (A2) to pull out the antipode to the left, obtaining the sugar for a negative integer. We have thus shown that faithfulness holds for the (1,1) case, since every such diagram is equal to some integer sugar.

The general case, where diagrams can have any number of wires on the left and right, comes down to transforming the diagram in matrix form, as explained in Episode 16. This step completes the proof that φ is faithful, and since we already know it is full, it is an isomorphism.

---

 

So far we have been identifying “numbers” with diagrams of a particular kind; those with one dangling wire on each end. In B this gave us the natural numbers, and in H it gives us the integers. But, as argued in Episode 17, there’s nothing particularly special about (1, 1) diagrams; well, maybe apart from the fact that both in B and H composition for (1,1) diagrams turns out to be commutative. Our obsession with the (1, 1) case is due to history—the traditional way of doing matrix algebra means the concept of ‘number” comes first, then the concept of “matrix”.

The complex numbers are a nice example where it makes sense to consider “numbers” as something different than (1,1) diagrams  A complex number can be written as an expression r + si where r, s are numbers and i is a formal entity that behaves like a number, but with the mysterious property i² = -1. The numbers r and s are sometimes called, respectively, the real component and imaginary components. What is important for us is that to describe a complex number, it suffices to keep track of two ordinary numbers.  Our intuition is that wires carry numbers, so it makes sense to carry a complex number with two wires, the first for the real piece, the second for the imaginary piece.

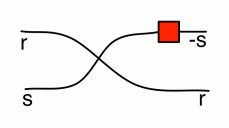
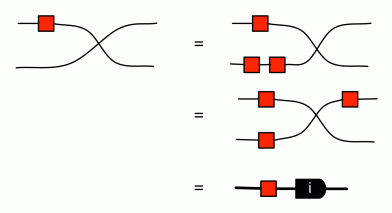
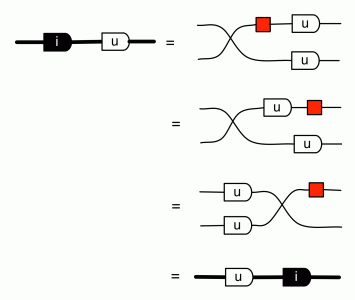
Now if we multiply a complex number r + si by i, we get (r + si)i = ri + sii = -s + ri. So what was the real component becomes the imaginary component, and the negative of what was the imaginary component becomes the real component. We have a diagram for that, and we have already seen it in this episode:

It thus makes sense to call this diagram i:

Now if we multiply r + si by an integer u, we get (r+si)u=ru + sui. So both the components are multiplied by u. We also have a diagram for that:

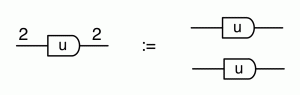
where on the right hand side we used the sugar for integers from the last episode.

For the rest of this section, to stop the proliferation of the digit 2 that clutters the diagrams, we will just draw the 2 wire using a thicker line, like so:

Now we can do some calculations. First if we compose the diagram for i with itself we get:

We can also show that i commutes with integers:

Following the general pattern of this blog,  we can ask what kinds of diagrams one can construct using the following gadgets.
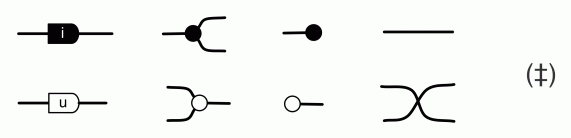Using our standard box of tricks for reasoning about diagrams, it is not difficult to show that the diagrams with one thick wire on each side will, in general, be of the form:

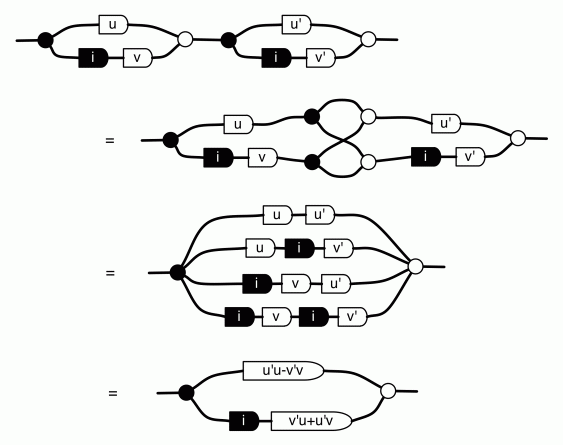
Composing two such entities gives us

which is of course what you’d get if you multiplied out two complex integers (those complex numbers u+vi where u and v are integers). In general, the diagrams that can be constructed from bricks (‡) are matrices with complex integer entries.

So what exactly is going on here? Let’s take a look under the hood.

The result is in matrix form, and corresponds to the 2×2 matrix:

and this is known as one way of representing complex numbers using matrices.

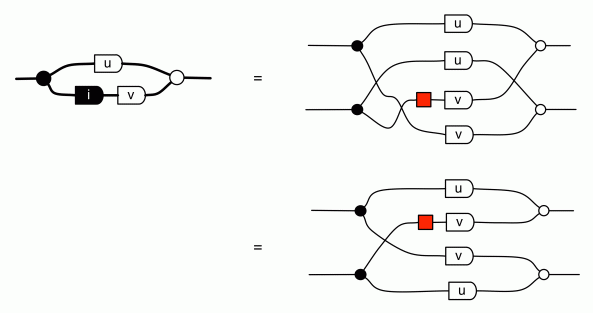
There is one more interesting thing to say here. Let’s take a look at the bizarro of i.

So the bizarro of i is -i. It follows that the bizarro of a general diagram constructed in the system (‡) corresponds to the operation known as conjugate transpose in complex matrix algebra.

If you know about quaternions, they can be considered in a similar way. Of course, we are constrained to integer coefficients for now. Not for long ☺.

---

 

I will give a 3 hour tutorial about graphical linear algebra at QPL ’15 in two chunks on Monday and Tuesday of next week. I’m desperately trying to get the slides done on time. Running this blog has been helpful in that it forced me to develop material, but unfortunately what we have covered so far will only be enough for around the first 30 mins; I should have started this blog back in January!

Continue reading with Episode 20 – Causality, Feedback and Relations.